Why Science Needs a New Correlation Model

The Quantitative Complexity Theory relies on a new, modern approach to correlation – the generalized correlation – which overcomes the well-known problems of mainstream approaches such as Pearson’s or Spearman’s correlation. The importance of correlation cannot be overstated. This is because the presence of a correlation implies the existence of a rule and rules are what make things work. By rules we mean something like: “if A then B”, or “if A then B, but only if C”. Every branch of science, but not only science, relies on determining correlations in order to prove hypothesis, to build theories, to discover new knowledge. Clearly, a structured and organized set of rules constitutes a piece of knowledge. This last phrase underscores the importance of structure, but this is a totally different discussion.

A few examples of immensely intricate interdependencies are illustrated below. The amount of detail and information these images convey is awesome. They are the result of simulations of complex physical phenomena, requiring intense computations with equally complex mathematical models. Would you treat them with a linear mindset? Can you imagine the loss of information and detail if you did? Wouldn’t it be a form of crime if you just forced straight lines over similar data?

In many cases, linear correlations are about the destruction of information, not the discovery of interdependencies. Take a look at the scatter plots below with an indubitably linear look and feel. The red line approximates what could be a linear regression model.

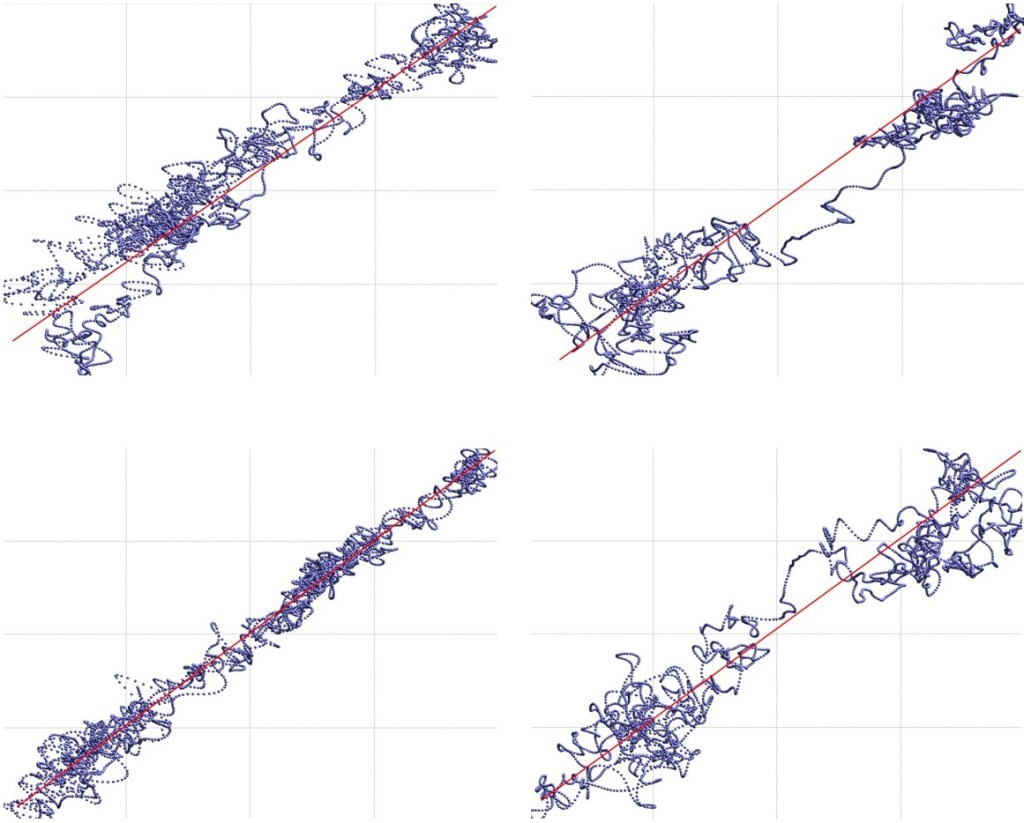
The biggest danger emerging from linear, even non-linear regression models, is that they induce a false sense of continuity and homogeneity. On a straight line, each point is equally important. Consider the two scatter plots on the right. There are evidently two clusters (attractors), where most of the data resides, while in the middle there is very little going on. A regression model doesn’t know that. And these are cases with a high linear correlation coefficient. But what about the other cases in the animated chart above, that do not have a linear look and feel?

Using linear correlations hides, however, another insidious form of danger, similar to drug addiction. If you use linear models long enough, you will think linearly, enjoying a placebo effect and false sense of control that linearity induces. Understanding Nature starts by explaining the interdependencies that make her tick. This is precisely why the QCT focuses so much on getting correlations right. It is not about ‘data science’. It’s about science.

PS. The best way to understand Nature is to understand her anomalies.