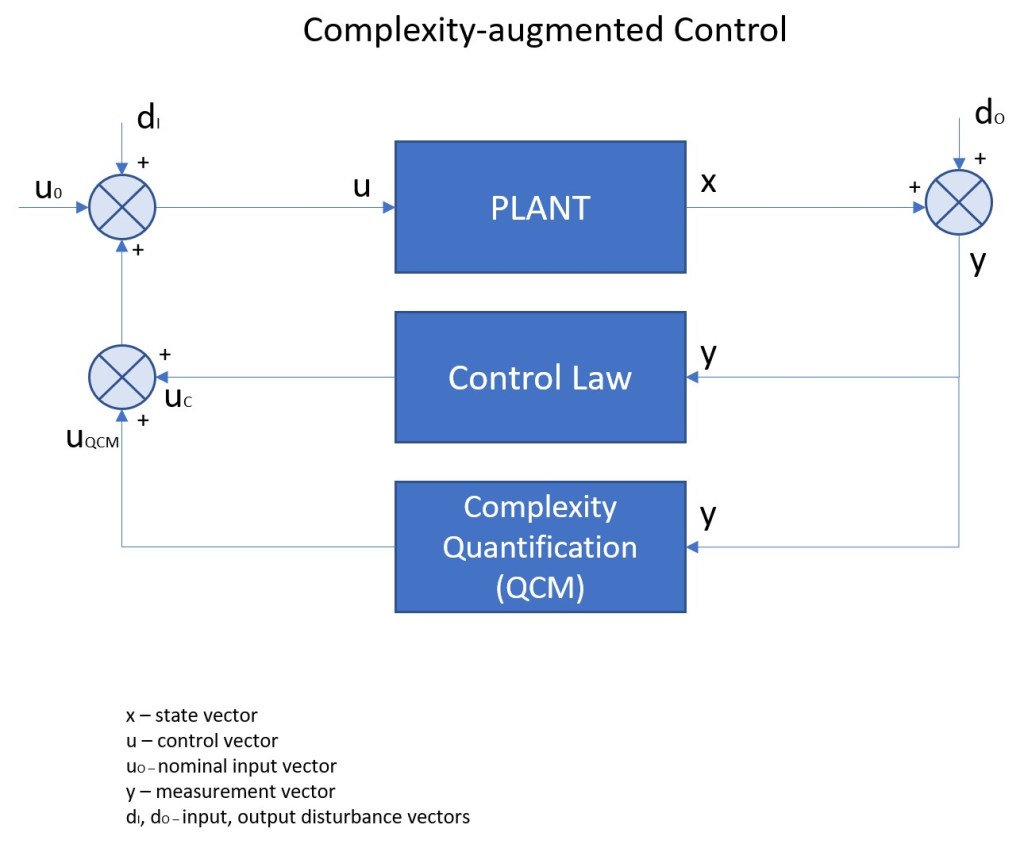
Complexity-based Augmentation of Control Systems

Complexity-based augmentation of conventional control systems means there is an additional control layer which produces feedback so as to drive a the complexity of given system to desired levels. The block diagram below illustrates the concept and shows the QCM component contributing to tradition feedback loop.

In essence, a complexity-based control system is an advanced hierarchical type of control system that adjusts its behavior based on the complexity of the environment, task, or system it is managing. Unlike traditional control systems that rely on fixed models or predefined rules, complexity-based control systems dynamically adapt to changing conditions by assessing and responding to different levels of complexity. This capability is important when it comes to delivering performance (and safety) in highly complex scenarios and situations which are saturated with uncertainty and disorder.

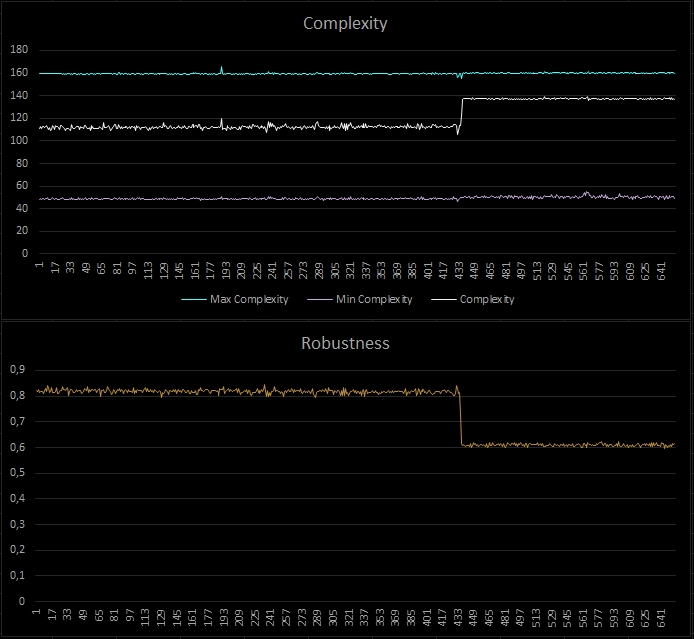
Because high complexity can lead to instability and fragility, the goal of QCM control is to drive complexity below prescribed thresholds and away from critical complexity. It is well known that in proximity of critical complexity robustness drops thereby increasing vulnerability. This is shown in the simple example below. The key point, though, is that you need to know your critical complexity and this is what QCM measures. In the chart below, critical complexity is indicated as “Max Complexity”.

In its simplest implementation, complexity-based control may simply mean switching control mode/type or adjusting control gains, so as to accomodate changes in the environment – e.g., low versus high-complexity traffic – or the system itself, e.g., cruise versus landing mode. This would give such a control system the characteristic of adaptability. The bottom line is higher resilience to uncertainty.

However, a more sophisticated goal of such a control strategy is to reduce the complexity of the controlled system, not just because of increased resilience in the traditional sense but because less complex system generally possess less failure modes and are less capable of delivering surprising behaviour.

The complexity-based gains are determined via a proprietary procedure which will not be described. However, for those who are familiar with, for example, LQG (Linear Quadratic Gaussian) control systems, one could minimize a cost function such as this:

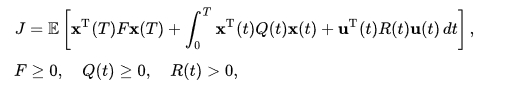
augmenting it with a quadratic complexity-specific component and solving a nonlinear differential Riccati matrix equation to yield the optimum feedback gains.

In alternative one could envisage a Hamiltonian-type of cost function in which Lagrange multipliers (co-states) are used to incorporate a complexity component. Adopting the PMP (Pontryaghin’s Maximum Principle) can yield an optimal controller.

However, our QCM control utilizes a proprietary approach in which time-dependent complexity-based feedback gains need not be determined via costly optimization.

So, QCM complexity-based control doesn’t have to be heuristic—it can be as quantitative as traditional control theory. By embedding real-time complexity analytics into control loops, systems gain the ability to predict, adapt, and optimize far beyond classical methods. Below is a comparison of traditional and complexity-based control systems.

How QCM Differs from Traditional Control Systems

Feature	Traditional Control	Ontonix-like QCM
Complexity Handling	Assumes fixed or bounded complexity	Dynamically measures and adapts to it
Metrics	Model-dependent	Model-free, data-driven
Adaptation	Rule-based or manual tuning	Autonomous, complexity-triggered
Failure Prediction	Often reactive	Proactive (via resilience thresholds)

As for applications, the possibilities are indeed numerous. Modern products, such as cars, aircraft, automated manufacturing plants, or defense systems, not to mention energy grids or traffic systems, are immensely complex and it is this inherent complexity that is creating a new class of problems. These systems tend to break down, for no apparent reason, and often the root cause is never identified. This is because conventional product design neglects complexity altogether – we have shown that complexity can indeed be a new, systemic, design attribute – and this is why future, high-tech products will have more problems tomorrow than they have today.

For this very reason, the presence of a QCM block, embedded in a conventional on-board control logic, can not only ensure that complexity stays beneath desired levels – ensuring systemic resilience and stability – it can also provide early-warnings of anomalies, functioning as an advanced monitoring system. It is this dual character of QCM, as a monitor and a controller, that makes it ideal for integration in modern, high-tech products and systems, as well as design strategies.

One day, Computer-Aided Engineering will take complexity into account, and products will be designed with complexity in mind from day one. Controller-product/system interaction will be taken into account from the very start, not a-posteriori, as is done traditionally.

Contact us for information.