How Credible are FE Car Crash Simulation Models?

Car crash simulation is performed by means of explicit Finite Element models, containing many millions of elements. These models are computationally intensive and parallel computing is used to perform the task. Evidently, the reason car crash is simulated in computers is to reduce and/or avoid expensive physical testing. Abundant literature is available on the subject.

The present blog will illustrate an example of how QCM technology can help evaluate and measure the credibility of finite element crash models. Clearly, in order to replace a physical test with a computer simulation, it is not only necessary for the simulation to reflect correctly the underlying physical phenomena, one must also know to what degree this is accomplished. The issue is addressed here.

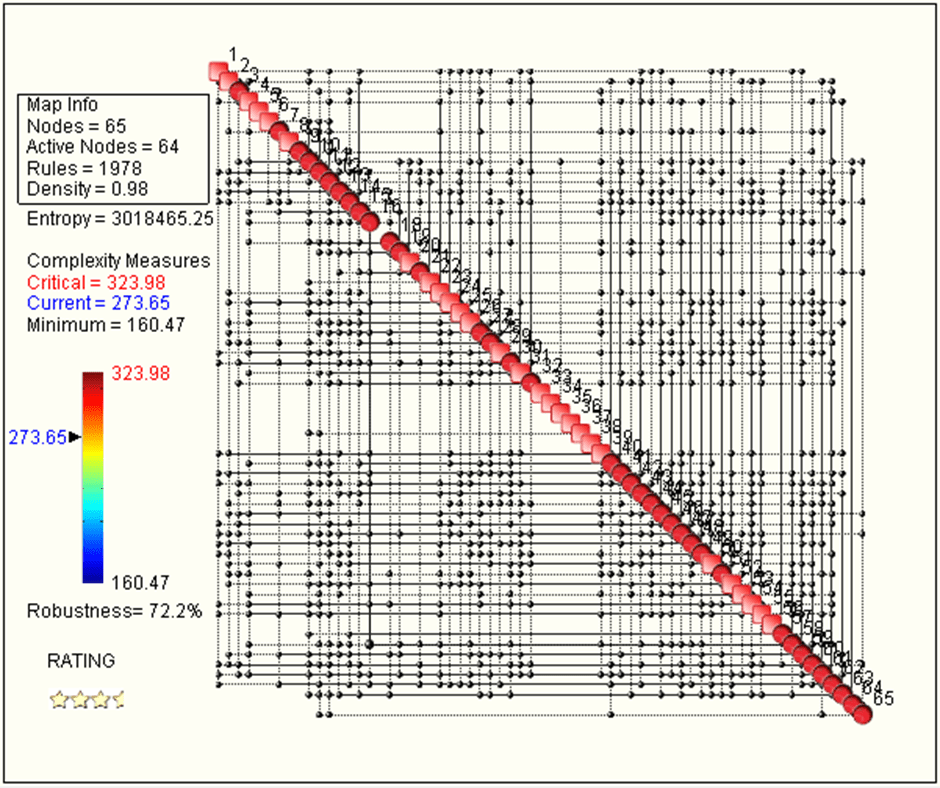
A physical crash test is performed, producing sensor outputs in 65 locations on the car. QCM produces the following Complexity Map, which shows the nearly 2000 interdependencies between the said 65 data channels. The map has a density of 98%, pointing to two things: 1) the phenomenon is complex and 2) probably some sensors are redundant.

In parallel, a crash test simulation is performed in the same configuration as the physical test and information is collected in the same 65 locations and with the same sampling frequency. The following Complexity Map is produced.

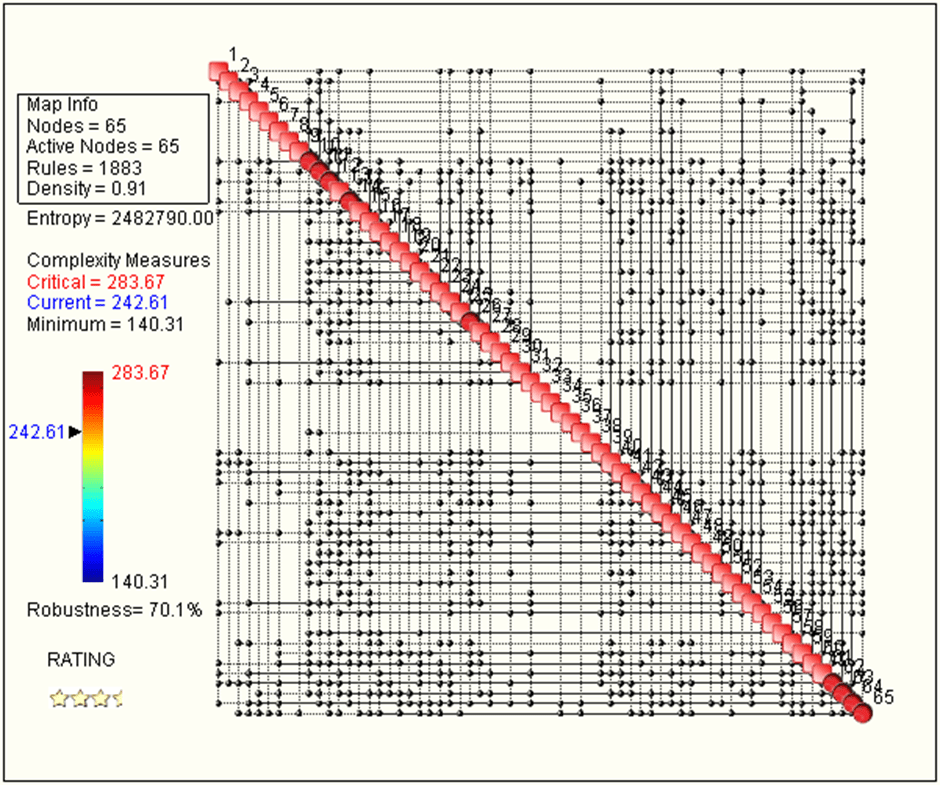
This time, map density is 91%, still very high but 7% less than the physical test.

There is an 11% difference in complexity, 18% difference in Total Entropy, and 7% difference in map density between the test and simulation cases.  Based on complexities, the model credibility can be quantified in 88%. In other words, the model misses approximately 12% of the total information contained in the test data. If the complexity between the two cases is “small”, the weak condition of model credibility is satisfied.

The strong condition of high model credibility is that the topologies of the test and simulation Complexity Maps be equal.  This can be verified by dividing the norm of the difference of the two maps (treated as matrices) by the norm of the test map.

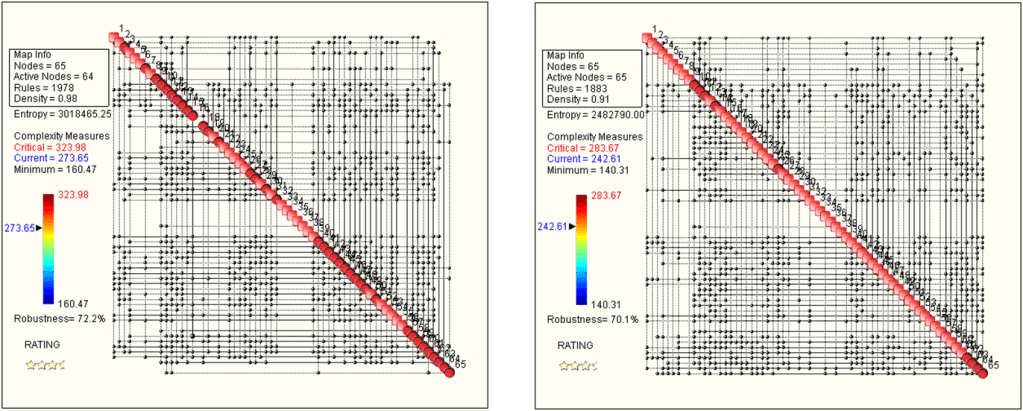
Test:   norm (CT) = 273.65

Simulation: norm (CS) = 242.61

Difference: norm |(CT –  CS)| = 82.48

Model Credibility Index = 1 –  norm |(CT –  CS)| / norm (CT)  = 1 – 82.48/273.65 = 0.698

Based on the above approach, it may be concluded that the simulation embraces approximately 70% of the test. In other words, the model neglects approximately 30% of what took place in the physical test.

In conclusions, based on the weak condition, the model correctly reproduces approximately 88% of the information contained in the test data.

Based on the strong condition – requiring topological similarity of the two complexity maps –  it may be concluded that the simulation embraces approximately 70% of the test. In other words, the model neglects approximately 30% of what took place in the physical test.

In the past we have used QCM to analyse numerous finite element crash models for various car manufacturers. The conclusion is that so far we have been unable to find a model which misses less than 20% of the physics of a real car crash.

The question this begs is this: is it really necessary to build computer models with disputable levels of detail, which require immense compute power, and still miss a large amount of physics? While this is done in the name of so-called “precision”, it is often forgotten that models must be realistic, not precise. There is no need to play extravagant video games.

PS. No Artificial Intelligence, no Machine Learning is needed to do this. All it takes is a single execution of OntoTest™.

PPS. You can apply this technique to any test-computer simulation case.